ランキングデータの法則性

この法則はよく知られています。

図RR-1は、ランキンググラフに累積グラフ（構成比：％　右側目盛）を重ねて表示したもので、パレート図と呼ばれます。この例では、上位20％（1位～10位）までの累積値は全体の64％です。 

この値はケースによって当然ですが異なります。しかしながら、相当ラフな表現ですが、分かりやすい数字でこれを「80対20の法則（パレートの法則）」と言います。僅かな数のデータで全体の大部分を占めるという特徴です。

注　：　ジップの法則とも言います。

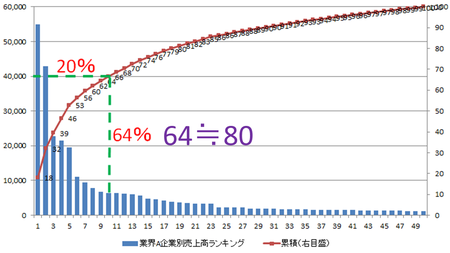
図RR-1　パレート図

通常は気にしていないかも知れませんが、ランキングデータには大きな格差があります。この大きな格差というのは企業活動におけるランキングデータの重要な特徴（法則性）の一つです。

図RR-2　大きな格差

図R-3のランキンググラフで明らかなように、順位が下がるにつれて少しずつ値が小さくなってます。ロングテール（長い尾のように見えることから）という名でよく知られています。 

これもランキングデータの重要な特徴で、例外を除いて　×　のようなパターンにはなりません。

図RR-3　ロングテール

業界Aの上位50社の平均売上高を考えてみます。1位は約55000、50位は約1000で、平均は約6000（12位あたり）です。平均値と各データに大きなかい離（1位は平均の10倍、下位は平均の1／10）があり、平均値というものに違和感があります。このような平均値は誤った判断を導くため、意味がありません。

注：　理論的には企業活動のランキングデータは統計学的な期待値（平均値）は計算できません（各サンプルからの計算値は収束せず、発散する）。

図RR-4　意味のない平均値

 図RR-5は、対数目盛に変換したものです。対数グラフでは、大きな均等目盛は一桁を表わし、中間の目盛は次第に幅が狭くなる変則目盛となっています。例えば横軸10（10位）のすぐ右側にある目盛は20（20位）を表わします。

このグラフで見ると、通常目盛グラフとは全く異なった形が見えてきます。全データが右下がり45度の直線に沿って並んでいることが見てとれます。あたかもこの直線にデータが縛りつけられているように見えるので、この直線を「縛り棒」と呼ぶことにします。全データがほぼ一直線上に並ぶこともあれば、複数の直線が現れることもあります。　

（注　：　①図R-5は25位以下が直線から下方に離れていますが、この説明では無視します　　②「縛り棒」はCARPES独自の表現です）。

また、直線上に並ぶということは、それぞれのデータ間に特別な秩序があるということになります。

注　：　直線が現れるデータ間の関係を専門用語でべき乗則といいます。

図RR-5　対数グラフによるランキング表示

縛り棒については、

◆何本の直線があるか

◆直線の傾き具合はどうか

◆どのように動くのか

が分析する上で非常に重要になります。ここでは簡単のために直線が1本の場合で説明します。 

過去のある年度における業界A売上高ランキングの縛り棒が赤の実線です。お互いが自由競争型の競争環境にある場合に傾きが45度付近になります。

ここから、例えば今年度のランキングを同じグラフに表示する場合を破線で表わすと、以下の3種の動きが考えられます。

◆図RR-6　平行移動　業界内の競争環境が変わらず、市場規模が拡大または縮小した場合には平行移動します。

◆図RR-7　急勾配　業界内の競争環境が寡占型の場合には急勾配となります。

◆図RR-8　緩勾配　業界内の競争環境が棲み分け型（談合型）の場合には緩い勾配になります。

図RR-9に変化の例を示します。EU加盟国（英国除く）の名目GDPランキングで1位はドイツです。2007年と2014年の比較で、着々とドイツによる寡占型EU経済支配へと進んでいる経済構造変化が如実に表れています。

ランキングデータには際だった特徴があります。例えば、業界Aの個々の企業についてその業績や行動をいくら仔細に調べても、業界全体が縛られる棒があるという特徴は決してわからないのです。個々の動きからは決してわからないこの全体としての秩序が出現します。

注　:　この現象を専門用語で創発と言います。

RR-10　不思議な秩序出現

人為的に操作されていない自然なデータの値は、その最高桁数字の出現頻度が理論的に下表のようになります。これをベンフォードの法則といいます。

表RR-1　ベンフォード理論値

図RR-11　ベンフォード理論値

もしデータがこの分布に従わない場合は、そのデータは何らかの制御あるいは悪意ある操作が行われている可能性が高いということになります。図RR-12（某社財務諸表のデータ）の場合、”5”の出現頻度が理論値の約2倍、”6”の出現頻度が理論値の1／3以下となっており、著しく理論値から乖離しているため、不正操作が疑われるデータです。

図RR-12　実データと理論値の比較